Travelling Salesman Problem
The Travelling Salesman Problem (TSP) is an optimisation problem in algorithmic research based on a simple scenario:
- A salesman must travel between N cities
- Cities are linked to other cities with a cost (e.g. journey distance or duration)
- The salesman does not care about order, just that they visit all cities
To solve TSP, our aim is to search for the lowest cost path connecting every node (city) in the graph (map). A simple method is to test every possible solution, but this is very slow; for N cities there are (N-1)! possible paths. This post investigates a more complex approach to solving TSP that tries to reach the solution without computing the massive solution space in its entirety.
Genetic Algorithms
Genetic algorithms (GA) are part of a biologically-inspired family of algorithms in ‘evolutionary computing’. The core idea in GAs is natural selection; individuals compete with each other to survive and reproduce. Selection is based on individual’s properties, which are encoded into ‘chromasomes’, to determine their fitness. Populations exist in generations that change every cycle - the fittest parents survive and reproduce (into modified children) while the unsuccessful parents, struggling for resources, die out. The steps are generalised like so:
- Initialise population of parents with random routes
- Reproduce parents to form children
- Modify the children’s chromasomes
- Evaluate the population and bin the least fit
- Loop steps 2 to 4 while maintaining the population size
Regarding TSP, the search space is every possible route between cities. Each chromasome is encoded with an order of cities. Fitness is calculated from the total distance between cities in a route.
Ideally, applying GA to solve TSP lets us find the solution (shortest route between cities) more quickly than testing the whole search space. In other words the population size * number of generations in the GA should be less than the ‘simple’ (N-1)! search.
Programmed Implementation
I practiced implementing a genetic algorithm to solve the Travelling Salesman Problem in openFrameworks/C++, using the following cities and distances:
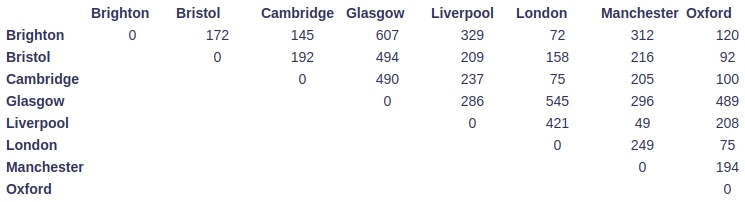
Initialising the population was as simple as:
// values/objects/containers
int populationSize = 40;
enum Cities { Brighton, Bristol, Cambridge, Glasgow, Liverpool, London, Manchester, Oxford };
typedef vector<Cities> route;
vector<route> routes;
// random population
auto rng = std::default_random_engine {};
for(int i=0; i<populationSize; i++)
{
route newRoute = {Brighton, Bristol, Cambridge, Glasgow, Liverpool, London, Manchester, Oxford};
std::shuffle(std::begin(newRoute), std::end(newRoute), rng);
routes.push_back(newRoute);
}To select parents to reproduce I implemented roulette wheel selection, which randomly chooses individuals using their fitness as the probability. My modification uses 1-point crossover that makes the child resemble part of both parents, and also individual mutation which makes a random change to the chromasome:
ofApp::route ofApp::modify(route parentA, route parentB)
{
route child;
// 1-point crossover
int crossoverPosition = ofRandom(1, 7); // split parents chromasomes
route parentB1(parentB.begin(), parentB.begin()+crossoverPosition);
route parentB2(parentB.begin()+crossoverPosition, parentB.end());
route parentA1(parentA.begin(), parentA.begin()+crossoverPosition);
for(auto city : parentB2) // add cities in B2 to A1
{
if(find(parentA1.begin(), parentA1.end(), city) == parentA1.end())
{
// add iff B2 city doesn't exist in A1 yet
parentA1.push_back(city);
}
else
{
// add another city to avoid duplication
for(int i=0; i<parentB.size(); i++)
{
if(find(parentA1.begin(), parentA1.end(), parentB[i]) == parentA1.end())
{
// city hasn't appeared already
parentA1.push_back(parentB[i]);
}
}
}
}
child = parentA1;
// mutation
int randomIndex1 = (int)ofRandom(0, 8); // choose 2 random elements
int randomIndex2 = (int)ofRandom(0, 8); // and swap them
iter_swap(child.begin() + randomIndex1, child.begin() + randomIndex2);
return child;
}The evaluation I implemented sorts the parents and children in order of their fitness, then picks the best half of each to be the next generation. This approach is called ‘steady-state GA’ as opposed to ‘generational GA’ where the whole population of parents would be replaced.
void ofApp::evaluate()
{
// order parents by fitness
routes = sortRoutes(routes);
// order children by fitness
nextRoutes = sortRoutes(nextRoutes);
// create new vector of the best half of the parents
vector<route> bestParentsAndChildren(routes.begin()+(populationSize/2),
routes.end());
// add best half of children to the vector
bestParentsAndChildren.insert(bestParentsAndChildren.end(),
nextRoutes.begin()+(populationSize/2), nextRoutes.end());
// clear and update the population for the next generation
routes.clear();
routes = bestParentsAndChildren;
}
vector<ofApp::route> ofApp::sortRoutes(vector<route> toSort)
{
// sort routes in order of fitness (distance)
int i=0;
while(i < populationSize-1){
i = 0;
for(int k=0; k<populationSize-1; k++)
{
if(getRouteDistance(toSort[k]) < getRouteDistance(toSort[k+1])){
swap(toSort[k], toSort[k+1]);
} else {
i++;
}
}
}
return toSort;
}Comment
The trial implementation found the shortest path to be 890 in length:
Glasgow->Liverpool->Manchester->Bristol->Oxford->Cambridge->London->Brightonwhich it reached in a fraction of the maximum possible (8-1)! = 5040 steps. It does this because, although the population is very small, they are constantly reproducing and the best genes are most likely to pass genes on. However, I had difficulty with C++ and know my code adds extra computational expense which sort of invalidates the optimisation.
Most of the crossover modification code is purely there to avoid adding duplicate cities. std::find for vectors is an NP-hard problem like TSP, and my crossover calls it several times for every new child. C++ has a std::set container which only stores unique elements which is better suited for the purpose. Additionally, my code evaluates fitness with getRouteDistance(route) every time it’s used (several times per individual per cycle). A better solution could use the std::map container to add routes together with their fitnesses. That way the fitness of each individual would be calculated just once. In general my encoding of the TSP problem itself is a problem.
Playing with the parameters and methods would be a useful development to better understand the problem and reduce (optimise) the number of generations taken before the solution is reached. I could switch the binning step to be generational (replace entire generation of parents each time), increase or decrease the amount of mutation (randomness) and do x-point crossover. Changes could also be made to the parent selection method which is one of many alternatives including Tournament selection. But until next time…
For Natural Computing (IS53052A)